Algorithm
记录
| 2020-07-14 | 2020-07-17 | 2020-07-19 | 2020-07-23 | |
|---|---|---|---|---|
| 283. 移动零 | ✅ | ✅ | ✅ | |
| 11. 盛最多水的容器 | ✅ | ✅ | ✅ | |
| 1. 两数之和 | ✅ | ✅ | ✅ | |
| 15. 三数之和 | ✅ | ✅ | ✅ |
16 号 ✌️ 跟 LJ 去修电脑,吃了小吃街嘻嘻
| 2020-07-15 | 2020-07-17 | 2020-07-20 | 2020-07-27 | |
|---|---|---|---|---|
| 206. 反转链表 | ✅ | ✅ | ✅ | |
| 92. 反转链表 II | ✅ | ✅ | ✅ | |
| 24. 两两交换链表中的节点 | ✅ | ✅ | ✅ | |
| 141. 环形链表 | ✅ | ✅ | ✅ |
| 2020-07-17 | 2020-07-19 | 2020-07-22 | 2020-07-26 | |
|---|---|---|---|---|
| 142. 环形链表 II | ✅ | ✅ | ||
| 25. K 个一组翻转链表 | ✅ | ✅ | ||
| 20. 有效的括号 | ✅ | ✅ | ||
| 155. 最小栈 | ✅ | ✅ |
| 2020-07-18 | 2020-07-20 | 2020-07-23 | 2020-07-27 | |
|---|---|---|---|---|
| 622. 设计循环队列 | ✅ | ✅ | ||
| 641. 设计循环双端队列 | ✅ | ✅ | ||
| 84. 柱状图中最大的矩形 | ✅ | ✅ | ✅ | |
| 239. 滑动窗口最大值 | ✅ | ✅ | ✅ |
| 2020-07-19 | 2020-07-21 | 2020-07-24 | 2020-08-09 | |
|---|---|---|---|---|
| 242. 有效的字母异位词 | ✅ | ✅ | ||
| 49. 字母异位词分组 | ✅ | ✅ | ||
| 94. 二叉树的中序遍历 | ✅ | ✅ | ✅ | |
| 144. 二叉树的前序遍历 | ✅ | ✅ | ✅ |
| 2020-07-20 | 2020-07-22 | 2020-07-25 | 2020-08-09 | |
|---|---|---|---|---|
| 590. N 叉树的后序遍历 | ✅ | ✅ | ||
| 589. N 叉树的前序遍历 | ✅ | ✅ | ||
| 429. N 叉树的层序遍历 | ✅ | ✅ | ✅ | |
| 22. 括号生成 | ✅ | ✅ | ✅ |
| 2020-07-21 | 2020-07-23 | 2020-07-26 | 2020-07-30 | |
|---|---|---|---|---|
| 226. 翻转二叉树 | ✅ | ✅ | ||
| 98. 验证二叉搜索树 | ✅ | ✅ | ||
| 104. 二叉树的最大深度 | ✅ | ✅ | ||
| 111. 二叉树的最小深度 | ✅ | ✅ | ✅ |
22 号 ✌️ 去拿电脑了,生产力回来了,LJ 去超市跟零食告别 👋
开始写项目了,后面随缘刷题了,等写好项目再好好刷
| 2020-07-28 | 2020-08-09 | 2020-10-14 | 2020- | 2020- |
|---|---|---|---|---|
| 297. 二叉树的序列化与反序列化 | ✅ | ✅ | ||
| 235. 二叉搜索树的最近公共祖先 | ✅ | ✅ | ||
| 236. 二叉树的最近公共祖先 | ✅ | ✅ |
| 2020-07-29 | 2020-08-09 | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 105. 从前序与中序遍历序列构造二叉树 | ✅ | |||
| 77. 组合 | ✅ | ✅ | ||
| 46. 全排列 | ✅ | ✅ | ||
| 47. 全排列 II | ✅ | ✅ |
| 2020-08-19 | 2020-10-15 | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 78. 子集 | ✅ | |||
| 50. Pow(x, n) | ✅ |
| 2020-08-20 | 2020-10-16 | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 169. 多数元素 | ✅ | |||
| 51. N 皇后 | ✅ | |||
| 17. 电话号码的字母组合 | ✅ |
| 2020-08-21 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 102. 二叉树的层序遍历 | ✅ | |||
| 515. 在每个树行中找最大值 | ✅ |
Vue3 源码看完了,继续刷题,准备面试
| 2020-10-11 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 752. 打开转盘锁 | ✅ | |||
| 433. 最小基因变化 | ✅ | |||
| 127. 单词接龙 | ✅ |
| 2020-10-12 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 200. 岛屿数量 | ✅ | |||
| 529. 扫雷游戏 |
| 2020-10-13 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 455. 分发饼干 | ✅ | |||
| 860. 柠檬水找零 |
| 2020-10-15 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 121. 买卖股票的最佳时机 | ✅ | |||
| 122. 买卖股票的最佳时机 II | ✅ |
| 2020-10-16 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 55. 跳跃游戏 | ||||
| 45. 跳跃游戏 II |
| 2020-10-17 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 69. x 的平方根 | ||||
| 367. 有效的完全平方数 |
| 2020-10-20 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 33. 搜索旋转排序数组 | ||||
| 34. 在排序数组中查找元素的第一个和最后一个位置 | ||||
| 74. 搜索二维矩阵 |
| 2020-10-22 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 62. 不同路径 | ||||
| 63. 不同路径 II | ||||
| 1143. 最长公共子序列 |
| 2020-10-23 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 120. 三角形最小路径和 | ||||
| 53. 最大子序和 | ||||
| 152. 乘积最大子数组 |
| 2020-10-24 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 198. 打家劫舍 | ||||
| 337. 打家劫舍 III |
| 2020-10-25 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 714. 买卖股票的最佳时机含手续费 | ||||
| 309. 最佳买卖股票时机含冷冻期 |
| 2020-10-26 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 208. 实现 Trie (前缀树) | ||||
| 212. 单词搜索 II | ||||
| 79. 单词搜索 |
| 2020-10-27 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 547. 朋友圈 | ||||
| 130. 被围绕的区域 |
| 2020-10-29 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 146. LRU 缓存机制 |
| 2020-11-10 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 1122. 数组的相对排序 |
| 2020-11-11 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 56. 合并区间 |
| 2020-11-14 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 771. 宝石与石头 | ||||
| 8. 字符串转换整数 (atoi) |
| 2020-11-16 | 2020- | 2020- | 2020- | 2020- |
|---|---|---|---|---|
| 541. 反转字符串 II | ||||
| 917. 仅仅反转字母 | ||||
| 125. 验证回文串 | ||||
| 680. 验证回文字符串 Ⅱ | ||||
| 5. 最长回文子串 |
数组、链表、跳表
- 283. 移动零:双指针
- 11. 盛最多水的容器:双指针,left > right 时,如果 left 不论右移多少,都比原来小,所以可以从两边双指针试
- 1. 两数之和:利用 Map 对一遍历过的数进行存储,如果
map.get(target - nums[i]) != null就得到结果 - 15. 三数之和:先排序,排序是为了去重,
nums[i] === nums[i - 1]就 continue,然后对于i + 1和nums.length - 1做双指针,当三数之和为 0 时就移动双指针,sum < 0 时就移动左指针,sum > 0 时就移动右指针 - 206. 反转链表:迭代、递归
- 92. 反转链表 II:迭代,双指针保留 m 和 m - 1,m 到 n 反转后进行连接
- 24. 两两交换链表中的节点:迭代、递归
- 141. 环形链表:双指针、哈希表
- 142. 环形链表 II:双指针、哈希表
- 25. K 个一组翻转链表:迭代、递归
栈、队列
哈希表
树
- 94. 二叉树的中序遍历
- 144. 二叉树的前序遍历
- 590. N 叉树的后序遍历
- 589. N 叉树的前序遍历
- 429. N 叉树的层序遍历
- 226. 翻转二叉树:迭代、递归
- 98. 验证二叉搜索树:递归、中序遍历
- 104. 二叉树的最大深度
- 111. 二叉树的最小深度:递归(DFS)、迭代(BFS 层序遍历、DFS)
- 297. 二叉树的序列化与反序列化:前序遍历、JSON 偷懒
- 235. 二叉搜索树的最近公共祖先
- 236. 二叉树的最近公共祖先:分治
- 105. 从前序与中序遍历序列构造二叉树
回溯
- 22. 括号生成:回溯(DFS)、BFS、动态规划
- 77. 组合:回溯
- 46. 全排列:回溯
- 47. 全排列 II:回溯(dfs)+ 剪枝
- 78. 子集:回溯
- 50. Pow(x, n):快速幂
- 169. 多数元素:哈希表、分治、投票
- 51. N 皇后:回溯
- 17. 电话号码的字母组合:回溯
DFS、BFS
- 102. 二叉树的层序遍历
- 515. 在每个树行中找最大值
- 752. 打开转盘锁:BFS、DFS
- 433. 最小基因变化:BFS、DFS
- 127. 单词接龙:BFS、DFS(超时)
- 200. 岛屿数量:BFS、DFS、并查集
- 529. 扫雷游戏:BFS、DFS
- 212. 单词搜索 II
- 79. 单词搜索
贪心
二分查找
69. x 的平方根:牛顿法、二分法
牛顿法: 的正的零点就是 的平方根
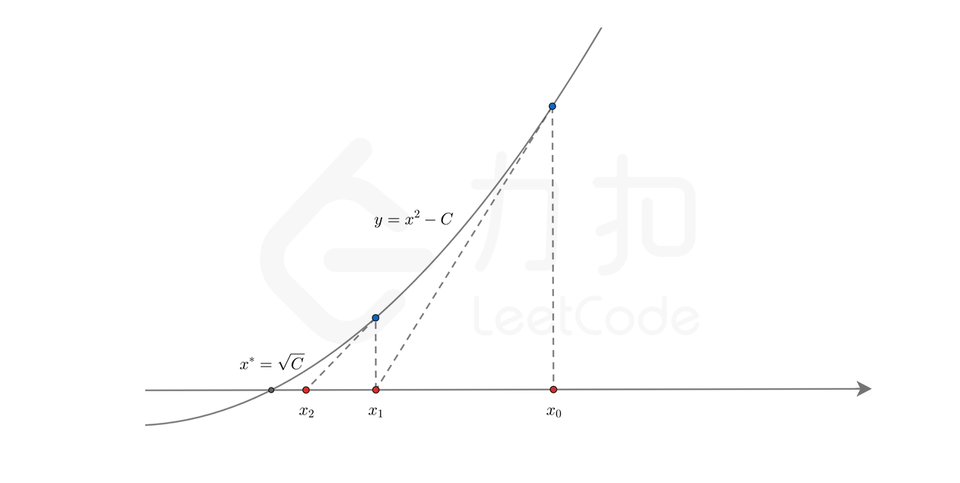 1var mySqrt = function(x) { // x 就是 C2 let res = x // res 从 x 开始逼近3 while (res * res > x) res = Math.floor((res + x / res) / 2)4 return res5};
1var mySqrt = function(x) { // x 就是 C2 let res = x // res 从 x 开始逼近3 while (res * res > x) res = Math.floor((res + x / res) / 2)4 return res5};
动态规划
递归法:自上而下,会有重复的计算
 1/**2 * @param {number[]} coins3 * @param {number} amount4 * @return {number}5 */6var coinChange = function(coins, amount) {7 let memo = new Map() // memo 进行优化8 function dp(n) {9 if (memo.has(n)) return memo.get(n)10 if (n === 0) return 011 if (n < 0) return -112 let res = Infinity13 for (let coin of coins) {14 let sub = dp(n - coin) // 子问题15 if (sub === -1) continue16 res = Math.min(res, 1 + sub) // 找最优解17 }18 memo.set(n, res)19 return res === Infinity ? -1 : res // 无解就返回 -120 }21 return dp(amount)22};
1/**2 * @param {number[]} coins3 * @param {number} amount4 * @return {number}5 */6var coinChange = function(coins, amount) {7 let memo = new Map() // memo 进行优化8 function dp(n) {9 if (memo.has(n)) return memo.get(n)10 if (n === 0) return 011 if (n < 0) return -112 let res = Infinity13 for (let coin of coins) {14 let sub = dp(n - coin) // 子问题15 if (sub === -1) continue16 res = Math.min(res, 1 + sub) // 找最优解17 }18 memo.set(n, res)19 return res === Infinity ? -1 : res // 无解就返回 -120 }21 return dp(amount)22};迭代法:自下而上
1/**2 * @param {number[]} coins3 * @param {number} amount4 * @return {number}5 */6var coinChange = function(coins, amount) {7 let dp = new Array(amount + 1).fill(amount + 1)8 dp[0] = 0 // amount 为 0 时解为 09 for (let i = 0; i < dp.length; i++) { // 从 amount 为 0 开始计算,自下而上计算10 for (let coin of coins) { // 遍历 coins11 let left = i - coin // 子问题的 amount12 if (left < 0) continue13 dp[i] = Math.min(dp[i], 1 + dp[left] /* 子问题的解 */) // 找最优解14 }15 }16 return (dp[amount] === amount + 1) ? -1 : dp[amount]17};假设 n 个节点存在的二叉搜索树有 G(n) 种,f(i) 为以 i 为根的二叉搜索树的个数
得到:
递归法:
1/**2 * @param {number} n3 * @return {number}4 */5let memo = [1, 1]6var numTrees = function(n) {7 if (m = memo[n]) return m8 let res = 09 for (let i = 1; i <= n; i++) {10 res += numTrees(i - 1) * numTrees(n - i) // 子问题11 }12 memo[n] = res13 return res14};迭代法:
1/**2 * @param {number} n3 * @return {number}4 */5var numTrees = function(n) {6 let dp = new Array(n + 1).fill(0)7 dp[0] = 1, dp[1] = 18 for (let m = 2; m <= n; m++) { // 2 ~ n 的解9 for (let i = 1; i <= m; i++) {10 dp[m] += dp[i - 1] * dp[m - i] // 子问题11 }12 }13 return dp[n]14};先看不需要求模的版本
1/**2 * @param {number} n3 * @return {number}4 */5var cuttingRope = function(n) {6 let dp = new Array(n + 1).fill(0)7 ;[dp[0], dp[1]] = [0, 1]8 for (let i = 2; i <= n; i++) { // 自下而上,先求 0 1 2... 的结果,求上去得到 n 的9 for (let j = 1; j <= i; j++) { // 剪多长10 dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j) // 剪了还剪、剪了就不剪了11 }12 }13 return dp[n]14};但是在需要求模时就不行了,因为 Math.max 不能正确比较出经过求模后的原来的最大值,如果先比较后求模又会溢出
所以可以用贪心:因为 1 和任何一个更大的数就有更大的,2 可以,3 可以,4 拆成两个 2 效果一样,5 可以拆成 2 * 3
1/**2 * @param {number} n3 * @return {number}4 */5var cuttingRope = function(n) {6 if (n < 3) return 17 if (n === 3) return 28 let res = 19 let mod = 100000000710 while (n > 4) {11 res = (res * 3) % mod12 n -= 313 }14 return (res * n) % mod15};对此就是求 3 的幂,可以使用快速幂进行进一步优化
因为 ,所以可以同时取余防止溢出
1// 递归快速幂2function qpow(a, n) { // a ** n3 if (n === 1) return 14 if (n % 2 === 1) return qpow(a, n - 1) * a % MOD5 let tmp = qpow(a, Math.floor(n / 2) % MOD)6 return tmp * tmp % MOD7}1// 迭代快速幂,7 ^ 10 = 7 ^ 0b1010 = 7 ^ 0b1000 * 7 ^ 0b102function qpow(a, n) {3 let res = 14 while (n > 0) {5 if ((n & 1) === 1) {6 res *= a7 res = res % MOD8 }9 a *= a // 相当于左移10 a = a % MOD11 n = n >> 112 }13 return res14}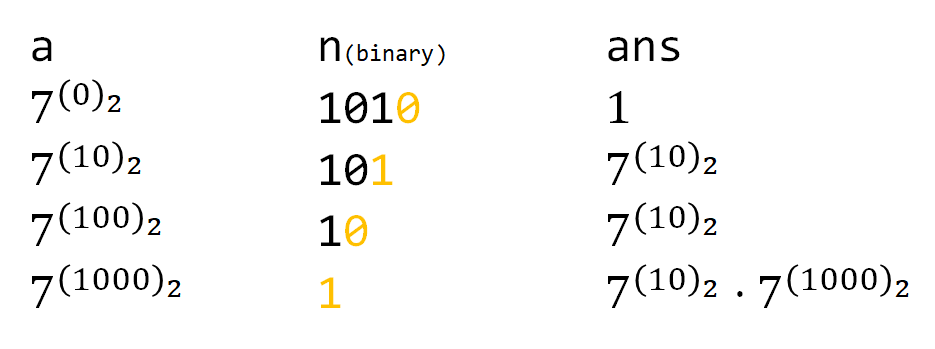
因为取余是为了防溢出,所以 JS 也可以使用 BigInt,最后取余(具体类似于前两个代码块版本,只不过 number 全都变为 BigInt,最后再取余)
字典树
并查集
LRU
数组和链表的不同
本质上是内存存储结构的不同,数组是一段连续的内存,链表是不连续的
由于数组是连续的,所以更适合通过下标访问:array[i]_address = base_address + i * data_type_size
而对于插入删除由于需要保证内存的连续性,就需要大量的移动,如果忽略其连续性,插入时直接把原来的元素移到最后面时间复杂度同样是 O(1),对于删除操作,在用到时再把多次删除集中到一起,移动一次
容器能否完全替代数组
容器的优势在于封装大量操作,支持动态扩容。由于动态扩容会有涉及内存申请和数据搬移,消耗性能,如果事先已知大小,那使用数组性能更好,对于底层框架开发性能更重要,对于业务开发,可维护性更重要
数组下标为什么从 0 开始
从内存上看,下标叫做 offset 更合适,如果从 1 开始,
array[i]_address = base_address + (i - 1) * data_type_size每次访问就需要多一个减法运算,CPU 就需要多一个减法指令历史原因,C 从 0 开始,之后的语言都效仿 C
LRU 缓存淘汰算法
LRU(Least Recently Used,最近最少使用),如果数据最近被访问过,那么将来被访问的几率也更高
单链表实现
一个单向链表,最近访问的放到头部,越接近尾部就是越早访问的,当有一个新的数据访问时,从头遍历:
如果有缓存,就删除缓存节点,并插入到头部
如果没有缓存
如果缓存未满,直接插到头部
如果满了,就先删除最后一个尾节点再插入到头部
需要遍历链表,时间复杂度为 O(n)
散列表实现
// TODO: 散列表实现
完全二叉树与堆的关系
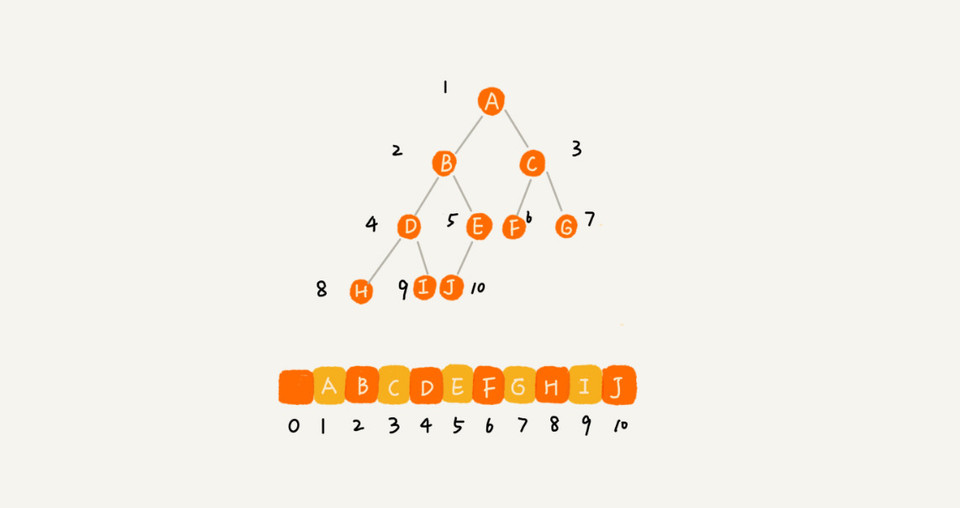
完全二叉树按层序遍历的顺序通过数组存储,浪费很少,堆就是完全二叉树
二叉搜索树如何删除
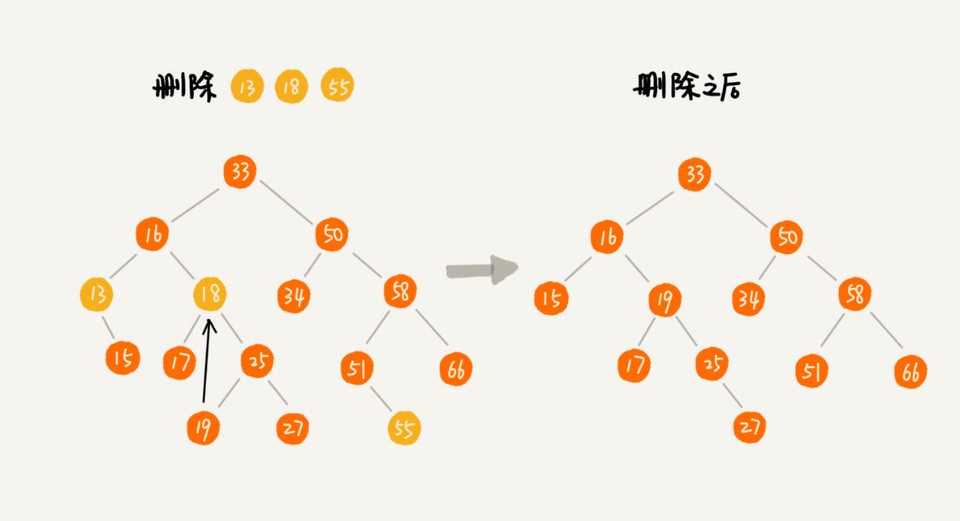
无子节点,直接删除
有一个子节点,用该子节点替换
两个子节点,用右子树的最小节点替换
有重复数据的二叉搜索树
存储的数据往往是个对象,需要一个 key 作为唯一标识,重复数据表示 key 相同的情况
通过链表把 key 相同的数据都存储在同一个节点上
把新的数据当作大于这个节点数据来处理。插入时放到节点右子树;查找时找到相同的之后继续在右子树中查找,返回所有查找到的;删除时将每个找到的节点跟上面的方式一样删除即可
散列表与二叉搜索树比较
散列表插入删除查找都是 O(1),而二叉查找树在比较平衡时插入删除查找才是 O(logn),为什么还要用二叉查找树?
散列表无序,二叉树中序遍历是有序的
散列表扩容耗时,需处理散裂冲突,二叉树性能稳定
散列表处理冲突,hash 函数耗时不一定比平衡二叉查找树快
散列表需要考虑散列函数的设计、冲突解决办法、扩容、缩容等,平衡二叉查找树只需考虑平衡性
排序
1// min: O(n), max: O(n^2)2// O(1) 原地排序3// 稳定4function bubbleSort(arr) {5 for (let i = 0; i < arr.length; i++) {6 let hasSwap = false7 for (let j = 0; j < arr.length - i - 1; j++) {8 if (arr[j] > arr[j + 1]) {9 [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]10 hasSwap = true11 }12 }13 if (!hasSwap) break14 }15 return arr16}1718// min: O(n), max: O(n^2)19// O(1) 原地排序20// 稳定21function insertSort(arr) {22 for (let i = 1; i < arr.length; i++) {23 let value = arr[i]24 let j = i - 125 for (; j >= 0; j--) {26 if (arr[j] > value) {27 arr[j + 1] = arr[j]28 } else break29 }30 arr[j + 1] = value31 }32 return arr33}3435// min: O(n^2), max: O(n^2)36// O(1)37// 不稳定38function selectSort(arr) {39 for (let i = 0; i < arr.length - 1; i++) {40 let index = i41 for (let j = i + 1; j < arr.length; j++) {42 if (arr[j] < arr[index]) {43 index = j44 }45 }46 [arr[index], arr[i]] = [arr[i], arr[index]]47 }48 return arr49}5051// min: O(nlogn), max: O(nlogn)52// O(n)53// 稳定54function mergeSort(arr) {55 return slice(0, arr.length - 1)5657 function slice(left, right) {58 if (left >= right) return59 let mid = Math.floor((left + right) / 2)60 slice(left, mid)61 slice(mid + 1, right)62 merge(left, mid, right)63 }64 function merge(left, mid, right) {65 let tmp = []66 let i = left, j = mid + 167 while (i <= mid && j <= right) {68 tmp.push(arr[i] < arr[j] ? arr[i++] : arr[j++])69 }70 while (i <= mid) tmp.push(arr[i++])71 while (j <= right) tmp.push(arr[j++])72 for (let k = 0; k < tmp.length; k++) {73 arr[left + k] = tmp[k]74 }75 }76}7778// min: O(nlogn), max: O(n^2), ava: O(nlogn)79// O(logn)80// 不稳定81function quickSort(arr) {82 return sort(0, arr.length - 1)8384 function sort(begin, end) {85 if (begin > end) return86 let pivot = partition(begin, end)87 sort(begin, pivot - 1)88 sort(pivot + 1, end)89 }90 function partition(begin, end) {91 let counter = begin, pivot = end92 for (let i = begin; i < end; i++) {93 if (arr[i] < arr[pivot]) {94 ;[arr[counter], arr[i]] = [arr[i], arr[counter]]95 counter++96 }97 }98 ;[arr[counter], arr[pivot]] = [arr[pivot], arr[counter]]99 return counter100 }101}102103// O(nlogn)104// O(1)105// not stable106function heapSort(arr) {107 if (arr.length === 0) return108 for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {109 heapify(arr, arr.length, i)110 }111 /**112 * heapPush: O(logn)113 * 8114 * 5 6115 * 1 3 0 2116 */117 for (let i = arr.length - 1; i > 0; i--) {118 ;[arr[0], arr[i]] = [arr[i], arr[0]]119 heapify(arr, i, 0)120 }121 /**122 * heapPop: O(logn)123 * 8 -> 2 | -> 6 |124 * 5 6 -> 5 6| -> 5 2|125 * 1 3 0 2 -> 1 3 0 |8 -> 1 3 0 |8126 */127 function heapify(arr, len, i) {128 let left = 2 * i + 1, right = 2 * i + 2129 let largest = i130 if (left < len && arr[left] > arr[largest]) {131 largest = left132 }133 if (right < len && arr[right] > arr[largest]) {134 largest = right135 }136 if (largest !== i) {137 ;[arr[largest], arr[i]] = [arr[i], arr[largest]]138 heapify(arr, len, largest)139 }140 }141}142143// max: O(nlogn) 一个桶, min: O(n) n 个桶144// 可以处理大量数据的情况,分桶存入内存处理145// 稳定性根据桶内的排序算法决定146function bucketSort(arr, bucketSize) {147 let max = Math.max(...arr)148 let min = Math.min(...arr)149 let bucketNum = Math.floor((max - min) / bucketSize) + 1150 let buckets = Array.from({ length: bucketNum }, _ => [])151 for (let i = 0; i < arr.length; i++) {152 let index = Math.floor((arr[i] - min) / bucketSize)153 buckets[index].push(arr[i])154 }155 let res = []156 for (let i = 0; i < bucketNum; i++) {157 res = res.concat(quickSort(buckets[i]))158 }159 return res160}161162// 类似桶排序,保证 n 个桶163// 负数和小数的情况下需要变为正数(+)和整数(*)164function countSort(arr) {165 let min = Math.min(...arr)166 let max = Math.max(...arr)167 let bucketNum = Math.floor((max - min) / 1) + 1168 let buckets = Array.from({ length: bucketNum }, _ => 0)169 for (let i = 0; i < arr.length; i++) {170 buckets[arr[i] - min] += 1171 }172 let res = []173 for (let i = 0; i < bucketNum; i++) {174 for (let j = 0; j < buckets[i]; j++) {175 res.push(i + min)176 }177 }178 return res179}180181// O(n)182// 适合位数很大的情况,比如手机号排序183function radixSort(arr) {184 let digit = `${Math.max(...arr)}`.length185 let start = 1186 while (digit) {187 start *= 10188 let buckets = []189 for(let i = 0; i < arr.length; i++) {190 const index = arr[i] % start191 !buckets[index] && (buckets[index] = [])192 buckets[index].push(arr[i])193 }194 arr = []195 for(let i = 0; i < buckets.length; i++) {196 buckets[i] && (arr = arr.concat(buckets[i]))197 }198 digit -= 1199 }200 return arr201}插入排序为什么比冒泡排序性能好
时间复杂度都是最差 O(n^2),最好 O(n),平均 O(n^2),但是冒泡是通过交换,交换需要三步,而插入是通过移动,移动需要一步
如何用快排思想在 O(n) 内查找第 K 大元素
通过 pivot 得到三个部分,小于 arr[pivot] 的,arr[pivot],大于 arr[pivot] 的,判断 pivot + 1 === K,是则返回 arr[pivot],大于则说明第 K 大的在 arr[0...pivot - 1] 中,递归继续查找,小于同理
二分查找变体
1// 查找第一个值等于给定值的元素2function binSearchFindFirst(arr, target) {3 let left = 04 let right = arr.length - 15 while (left <= right) {6 let mid = Math.floor((left + right) / 2)7 if (target > arr[mid]) left = mid + 18 else if (target < arr[mid]) right = mid - 19 else {10 if (mid === 0 || arr[mid - 1] !== target) return mid11 else right = mid - 112 }13 }14 return -115}1617console.log(binSearchFindFirst([1, 3, 4, 5, 6, 8, 8, 8, 11, 18], 8))1819// 查找最后一个值等于给定值的元素20function binSearchFindLatest(arr, target) {21 let left = 022 let right = arr.length - 123 while (left <= right) {24 let mid = Math.floor((left + right) / 2)25 if (target > arr[mid]) left = mid + 126 else if (target < arr[mid]) right = mid - 127 else {28 if (mid === arr.length - 1 || arr[mid + 1] !== target) return mid29 else left = mid + 130 }31 }32 return -133}3435console.log(binSearchFindLatest([1, 3, 4, 5, 6, 8, 8, 8, 11, 18], 8))3637// 查找第一个大于等于给定值的元素38function binSearchFindFirstGreaterEqual(arr, target) {39 let left = 040 let right = arr.length - 141 while (left <= right) {42 let mid = Math.floor((left + right) / 2)43 if (arr[mid] >= target) {44 if (mid === 0 || arr[mid - 1] < target) return mid45 else right = mid - 146 } else left = mid + 147 }48 return -149}5051console.log(binSearchFindFirstGreaterEqual([3, 4, 6, 7, 10], 5))5253// 查找最后一个小于等于给定值的元素54function binSearchFindLatestLessEqual(arr, target) {55 let left = 056 let right = arr.length - 157 while (left <= right) {58 let mid = Math.floor((left + right) / 2)59 if (arr[mid] <= target) {60 if (mid === arr.length - 1 || arr[mid + 1] > target) return mid61 else left = mid + 162 } else right = mid - 163 }64 return -165}6667console.log(binSearchFindLatestLessEqual([3, 4, 6, 8, 9, 10], 7))堆排序
1// i 到 n 进行堆化2function heapify(arr, n, i) {3 while (true) {4 let maxPos = i5 if (i * 2 <= n && arr[i] < arr[i * 2]) maxPos = i * 26 if (i * 2 + 1 <= n && arr[maxPos] < arr[i * 2 + 1]) maxPos = i * 2 + 17 if (maxPos === i) break8 ;[arr[i], arr[maxPos]] = [arr[maxPos], arr[i]]9 i = maxPos10 }11}1213function heapSort(arr) {14 function buildHeap(arr) {15 for (let i = Math.floor(arr.length / 2); i > 0; i--) {16 heapify(arr, arr.length, i)17 }18 }19 buildHeap(arr)20 let k = arr.length - 121 while (k > 1) {22 ;[arr[1], arr[k]] = [arr[k], arr[1]]23 k -= 124 heapify(arr, k, 1)25 }26 return arr27}2829// arr[0] 没用,只是从 1 开始方便计算30console.log(heapSort([0, 1, 3, 2, 5, 4, 2, 1, 0]))