编译原理之美

实现脚本语言

词法分析：把程序分割成一个个 Token 的过程，可以通过构造有限自动机来实现
语法分析：把程序的结构识别出来，并形成一棵便于由计算机处理的抽象语法树。可以用递归下降的算法来实现
语义分析：消除语义模糊，生成一些属性信息，让计算机能够依据这些信息生成目标代码

词法分析器

实现一个词法分析器，首先需要写出每个词法的正则表达式，并画出有限自动机，之后，只要用代码表示这种状态迁移过程就可以了

有限状态自动机 $M = (Σ, S, q_0, F, δ)$ ，分别是字符集、状态集、初始状态、终结状态（集）、转移函数

确定状态有限自动机 DFA：对任意字符，最多有一个状态可以转移， $F$ 是终结状态
非确定状态有限自动机 NFA：对任意字符，有多于一个状态可以转移， $F$ 是终结状态集

1Thompson 算法      子集构造算法      Hopcraft 最小化算法
2RE ------------> NFA ----------> DFA -----------------> 最小化 DFA ------> 词法分析器代码

RE -> NFA

e -> 𝛆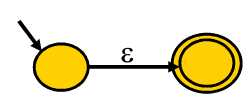
e -> c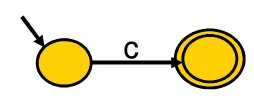
e -> e1 e2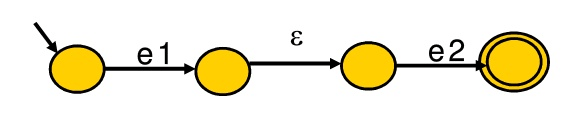
e -> e1 | e2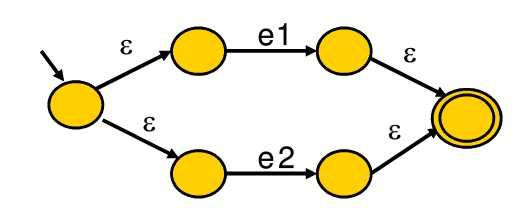
e -> e1*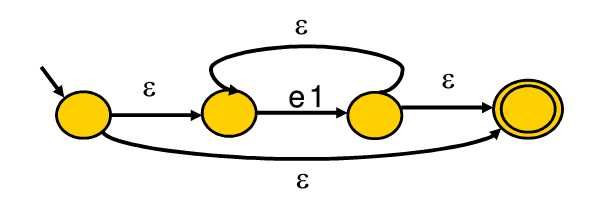

由上面构造 a(b|c)* 得

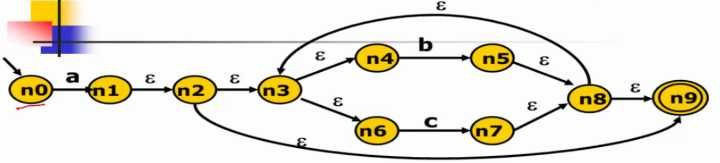
NFA -> DFA

1// eps_closure 可用 BFS 或 DFS 实现
2q0 <- eps_closure(n0)   // q0 = {n0}
3Q <- {q0}       // Q = {q0}
4workList <- q0     // workList = [q0, ...]
5while(workList != [])   
6  remove q from workList   // workList = [...]
7  foreach(character c)     // c = a
8    t <- e-closure(delta(q,c))   // delta(q0, a) = {n1}, t = {n1, n2, n3, n4, n6, n9}
9    D[q,c] <- t    //   q1 = t
10    if(t not in Q)    // Q = {q0, q1} , workList = [q1]
11      add t to Q and workList

a(b|c)* 进行转换可得

q1 = {n1, n2, n3, n4, n6, n9} q2 = {n5, n8, n9, n3, n4, n6} q3 = {n7, n8, n9, n3, n4, n6}

图像：

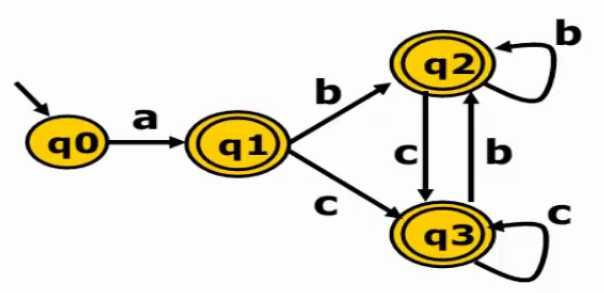
Hopcraft 最小化算法将 DFA 转化为最小化 DFA

1//基于等价类的思想
2split(S)
3  foreach(character c)
4    if(c can split s)
5      split s into T1, ..., Tk
6
7hopcroft()
8  split all nodes into N, A
9  while(set is still changes)
10    split(s)

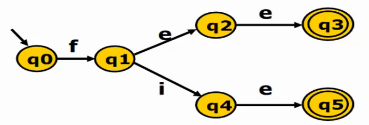
先分为非终结状态 N: {q0, q1, q2, q4} 和终结状态 A: {q3, q5}，在 N 中 q0 和 q1 在接受 e 的条件下最终得到的状态还是在 N 的内部。所以可以将其根据 e 拆分成 {q0, q1}，{q2, q4}，{q3, q5}。q0 和 q1 ，在接受 e 的时候，q0 最终得到还是在 {q0, q1} 这个状态的结合中，q1 却会落在 {q2, q4} 的状态中，所以可以将 q0 和 q1 分为 {q0}，{q1}

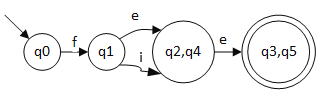
语法分析器

上下文无关文法

上下文无关文法 G 是一个四元组： $G = (T, N, P, S)$

T 是终结符集合
N 是非终结符集合
P 是一组产生式规则集合
S 是唯一的开始符号（非终结符，S ∈ N）

1E -> num
2   | id
3   | E + E
4   | E * E
5
6T = {num, id, +, *}
7N = {E}
8P = {E -> num, E -> id, E -> E + E, E -> E * E}
9S = E

推导

最左推导：每次总是选择最左侧的符号进行替换
最右推导：每次总是选择最右侧的符号进行替换

语法分析器的任务：语法分析器从记号流中获取句子 S，再接受使用上下文无关文法 G 描述的语言的语言规则，回答在 G 中是否存在对 S 的推导。是或者否。并给程序员反馈精确的出错信息

分析树

推导可以表达成树状结构
- 和推导所用的顺序无关（最左、最右、其它）
特点：
- 树中的每个内部节点代表非终结符
- 每个叶子节点代表终结符
- 每一步推导代表如何从双亲节点生成它的直接孩子节点

1E -> num
2   | id
3   | E + E
4   | E * E
5
6推导 3 + 4 * 5
7
8E -> E + E                  E
9  -> 3 + E           E      +      E
10  -> 3 + E * E       3          E  *  E
11  -> 3 + 4 * e                  4     5
12  -> 3 + 4 * 5
13
14E -> E * E                     E
15  -> E + E * E          E      *      E
16  -> 3 + E * E       E  +  E          5
17  -> 3 + 4 * E       3     4
18  -> 3 + 4 * 5
19
20得到两种树的结构，分析树的含义取决于树的**后序遍历**的顺序，所以第一个是先乘后加，第二个是先加后乘，导致二义性

二义性文法

重写解决

1E -> E + T
2   | T
3T -> T * F
4   | F
5F -> num
6   | id
7
8推导 3 + 4 * 5 如下
9
10E -> E + T                    E
11  -> T + T             E      +      T
12  -> F + T             T          T  *  F
13  -> 3 + T             F          F     5
14  -> 3 + T * F         3          4
15  -> 3 + F * F
16  -> 3 + 4 * F
17  -> 3 + 4 * 5
18
19推导 3 + 4 + 5 如下
20
21E -> E + T                       E
22  -> E + T + T            E      +      T
23  -> T + T + T         E  +  T          F
24  -> F + T + T         T     F          5
25  -> 3 + T + T         F     4
26  -> 3 + F + T         3
27  -> 3 + 4 + T
28  -> 3 + 4 + F
29  -> 3 + 4 + 5
30
31使用了左递归的方式（E -> E + T，T -> T * F ），从而使得该句子的计算顺序是 (3+4)+5，保证了加法的左结合性

算法

回溯算法（自顶向下）
递归下降分析算法：O(n)，容易实现（方便手工编码），错误定位和诊断信息准确，GCC4、LLVM 使用

1S -> N V N
2N -> s
3   | t
4   | g
5   | w
6V -> e
7   | d
8
9parse_S()
10  parse_N()
11  parse_V()
12  parse_N()
13
14parse_N()
15  token = tokens[i++]
16  if(token == s || token == t || token == g || token == w)
17    return;
18  error("...")
19
20parse_V()
21  token = tokens[i++]
22  ... //

一般框架：

1X -> β11 ... β1i
2   | β21 ... β2j
3   | β31 ... β3k
4   | ...
5
6parse_X()
7  token = nextToken()
8  switch(token)
9    case ...:  // β11 ... β1i
10    case ...:  // β21 ... β2j
11    case ...:  // β31 ... β3k
12    ...
13    default: error("...");

LL(1) 分析算法

从左（L）向右读入程序，最左（L）推导，采用一个（1）前看符号

与回溯算法不同的在于，又一个分析表进行优化，时间复杂度 O(n)

如何构造分析表就是关键，分别求出 NULLABLE 集合、FIRST 集合、FOLLOW 集合，然后推出 SELECT 集合，即预测分析表

NULLABLE 集合

1NULLABLE = {}
2while (NULLABLE is still changing)
3  for (production p: X -> β)
4    if (β == 𝛆)
5      NULLABLE ⋃= {X}
6    if (β == Y1Y2...Yn)
7      if (Y1 ∈ NULLABLE && ... && Yn ∈ NULLABLE)
8        NULLABLE ⋃= {X}

FIRST 集合

1for (noterminal N)
2  FIRST(N) = {}
3
4while (some set is still changing)
5  for (production p: N -> β1β2...βn)
6    for (βi from β1 upto βn)
7      if (βi == a)
8        FIRST(N) ⋃= {a}
9        break
10      if (βi == M)
11        FIRST(N) ⋃= FIRST(M)
12        if (M is not in NULLABLE)
13          break

FOLLOW 集合

1for (noterminal N)
2  FOLLOW(N) = {}
3
4while (some set is still changing)
5  for (production p: N -> β1β2...βn)
6    tmp = FOLLOW(N)
7    for (βi from βn downto β1)
8      if (βi == a)
9        tmp = {a}
10      if (βi == M)
11        FOLLOW(M) ⋃= tmp
12        if (M is not in NULLABLE)
13          tmp = FIRST(M)
14        else
15          tmp ⋃= FIRST(M)

SELECT 集合

1for (production p)
2  SELECT(p) = {}
3
4for (production p: N -> β1β2...βn)
5  for (βi from β1 upto βn)
6    if (βi == a)
7      SELECT(p) ⋃= {a}
8      return
9    if (βi == M)
10      SELECT(p) ⋃= FIRST(M)
11        if (M is not in NULLABLE)
12          return
13  SELECT(p) ⋃= FOLLOW(N)

例子：

1p0: Z -> d
2p1:    | X Y Z
3p2: Y -> c
4p3:    | 𝛆
5p4: X -> Y
6p5:    | a
7
8NULLABLE = {Y, X}
9
10N\FIRST  0  1      2
11Z        {} {d}    {d, c, a}
12Y        {} {c}    {c}
13X        {} {c, a} {c, a}
14
15N\FOLLOW 0  1
16Z        {} {}
17Y        {} {d, c, a}
18X        {} {d, c, a}
19
20        p0   p1         p2   p3         p4         p5
21SELECT  {d}  {d, c, a}  {c}  {d, c, a}  {d, c, a}  {a}
22
23预测分析表
24    a      c      d
25Z   p1     p1     p0,p1
26Y   p3     p2,p3  p3
27X   p4,p5  p4     p4

得到的预测分析表有的会有多个，引起冲突，导致算法的不确定性

1p0: E  -> T E'
2p1: E' -> + T E'
3p2:     | 𝛆
4p3: T  -> F T'
5p4: T' -> * F T'
6p5:     | 𝛆
7p6: F  -> ( E )
8p7:     | a
9
10NULLABLE = {E', T'}
11
12FIRST(E) = FIRST(T) = FIRST(F) = {(, a}
13FIRST(E') = {+, 𝛆}
14FIRST(T') = {*, 𝛆}
15
16FOLLOW(E) = FOLLOW(E') = {), #}
17FOLLOW(T) = FOLLOW(T') = {+, ), #}
18FOLLOW(F) = {*, +, ), #}
19
20预测分析表
21   a    +    *    (    )    #
22E  p0             p0
23E'      p1             p2   p2
24T  p3             p3
25T'      p5   p4        p5   p5
26F  p7             p6

解决冲突

消除左递归

1E -> E + T // 左递归情况下，E 能推导出 E 开头的，导致冲突
2   | T
3
4// T + T + T ... + T，把 `+ T` 看作一体，重新构建成右递归的形式
5
6E -> T E'
7E' -> + T E'

提取左公因子

1X -> a Y
2   | a Z // 都是 a 开头，导致冲突
3
4X -> a X'
5X' -> Y
6    | Z