信息的表示与处理
信息存储
位 bit:二进制数字
字节 byte:8 位的块
机器级程序视存储器为一个非常大的字节数组,称为虚拟存储器,下标就是地址,所有可能地址的集合就是虚拟地址空间,编译器和运行时将存储器分为可管理的单元,来存放程序对象(数据、指令、控制信息),对于不同单元的分配和管理在虚拟地址空间中完成
16 进制
116 进制:0x 8 F 7 A 9 322 进制: 1000 1111 0111 1010 1001 0011116 进制:0x C 4 E 5 D22 进制: 1100 0100 1110 0101 110112 进制: 1011 0111 1001 1100216 进制:0x B 7 9 C12 进制: 11 0101 1011 0111 1110 0110216 进制:0x 3 5 B 7 E 616 进制的 0 代表 4 个 2 进制的 0,可以把 中的 写成 的形式,得到 的 16 进制为: 后面跟 个 0
| (十进制) | (十六进制) | |
|---|---|---|
| 11 | 2048 | 0x800(3 + 4 * 2) |
| 7 | 128 | 0x80(3 + 4 * 1) |
| 13 | 8129 | 0x2000(1 + 4 * 3) |
十进制转换为十六进制:76 = 4 * 16 + 12(C), 4 = 0 * 16 + 4(4), 76 => 0x4C
| 十进制 | 二进制 | 十六进制 |
|---|---|---|
| 243 | 11110011 | 0xF3 |
| 55 | 110111 | 37 |
字
字长:32 位、64 位,字长为 n 位的机器其虚拟地址范围是 ~ ,程序最多访问 字节,比如 32 位计算机虚拟地址空间为
数据大小
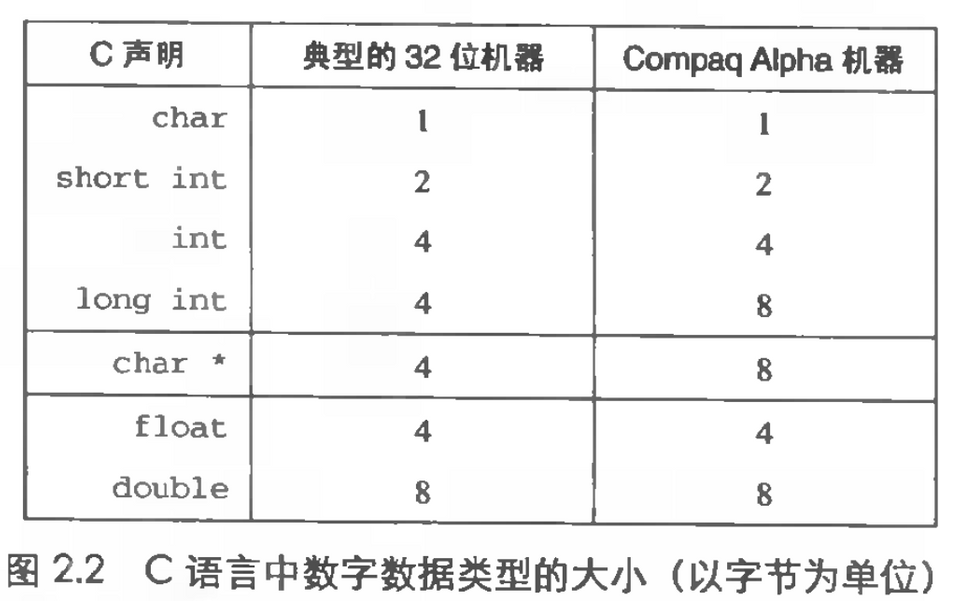
寻址和字节顺序
int 类型地址在 0x100,存 0x01234567:
1大端法: 0x100 0x101 0x102 0x1032 01 23 45 6734小端法: 0x100 0x101 0x102 0x1035(Intel) 67 45 23 011#include <stdio.h>2#include <stdlib.h>34typedef unsigned char *byte_pointer; // 定义类型56void show_bytes(byte_pointer start, int len) {7 int i;8 for (i = 0; i < len; i++)9 printf(" %.2x", start[i]);10 printf("\n");11}1213void show_int(int x) {14 show_bytes((byte_pointer) &x, sizeof(int));15}1617void show_float(float x) {18 show_bytes((byte_pointer) &x, sizeof(float));19}2021void show_pointer(void *x) {22 show_bytes((byte_pointer) &x, sizeof(void *));23}2425int main(int argc, char *argv[]) { // argc 命令行参数个数,argv 命令行参数26 printf(" %s\n", argv[1]);2728 int int_value = atoi(argv[1]); // char * 转 int29 float float_value = (float) int_value; // 强制类型转换30 int *pointer_value = &int_value;3132 show_int(int_value);33 show_float(float_value);34 show_pointer(pointer_value);3536 return 0;37}1$ gcc byte_pointer.c -o byte_pointer2$ byte_pointer 123453 123454 39 30 00 005 00 e4 40 466 7c 32 6d e2 fe 7f 00 00int 12345 十六进制是 0x00003039,float 12345 表示为 0x4640E400,其中有 13 位相匹配

表示字符串
C 中字符串以 null(\0)结尾,ASCII 码中 0x00 表示 \0,十进制数字 n 由 0x3n 表示,A~Z 由 0x41~0x5A 表示,man ascii 可以得到 ASCII 表
1char *s = "ABCDEF";2show_bytes((byte_pointer) s, strlen(s));3// 41 42 43 44 45 46ASCII 只适用于编码英语,编码其他特殊字符和语言需要 Unicode
表示代码
代码会被编译生成字节表示的机器代码,程序仅仅是字节序列
布尔代数和环
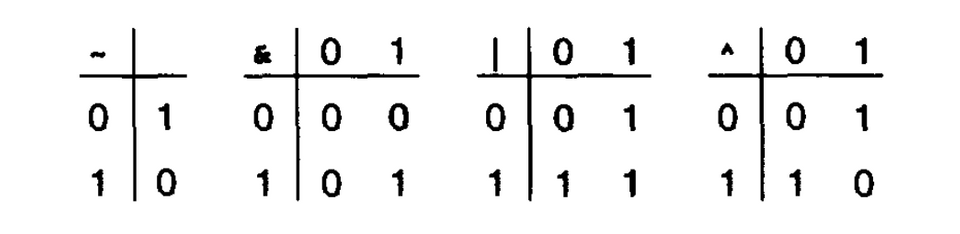
| 运算 | 结果 |
|---|---|
| a | 01101001 |
| b | 01010101 |
| ~a | 10010110 |
| ~b | 10101010 |
| a&b | 01000001 |
| a|b | 01111101 |
| a^b | 00111100 |
C 中的位级运算
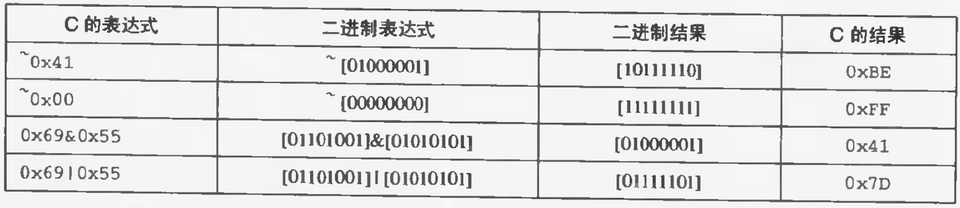
1void inplace_swap(int *x, int *y) {2 *x = *x ^ *y;3 *y = *x ^ *y; // *x ^ *y ^ *y == *x4 *x = *x ^ *y; // *x ^ *y ^ *x == *y5}C 中的逻辑运算
零表示 false,非零表示 true
C 中的移位运算
逻辑移位:补 0
算数移位:补最高(低)有效位
通常是逻辑左移和算数右移
| x | x << 3 | x >> 2(逻辑) | x >> 2(算数) |
|---|---|---|---|
| 0xF0 - 11110000 | 0x80 - 10000000 | 0x3C - 00111100 | 0xFC - 11111100 |
整数表示
整型数据类型
char: -128 ~ 127 unsigned char: 0 ~ 255 (, 1 bytes) short: -32768 ~ 32767 unsigned short: 0 ~ 65535 (, 2 bytes) int: -2147483648 ~ 2147483647 unsigned int: 0 ~ 4294967295 (, 4 bytes) long: (4 bytes) long long: (8 bytes)
无符号与补码
| x | 无符号 | 补码 |
|---|---|---|
| 0xA - 1010 | ||
| 0x8 - 1000 | ||
| 0xF - 1111 |
原码:最高位表示符号 6 - 0 000 0110 -6 - 1 000 0110
反码:正数同原码,负数除符号位取反 -6 - 1 111 1001
补码:计算机表示方式,正数同原码,负数取反码加一 -6 - 1 111 1010
C 有符号数转无符号数
运算时会隐式的把有符号数转换为无符号数
截断数字
1int x = 53191;2short y = (short) x; // -123453int z = y; // -12345x 对应 0000 0000 0000 0000 1100 1111 1100 0111 截断成 1100 1111 1100 0111,符号位是 1 所以是负的,100 1111 1100 0111 是 12345 的补码(减一取反的原码)
整数运算
补码加法
会溢出
假定长度是 4 位
正溢出:7 + 5 = 0111 + 0011 = 1010 = -2
负溢出:-8 + -5 = 1000 + 1011 = 0011 = 3
补码的非
5 = 0101 取反 1010 = () = -6 加一 1011 = -5
补码的乘法
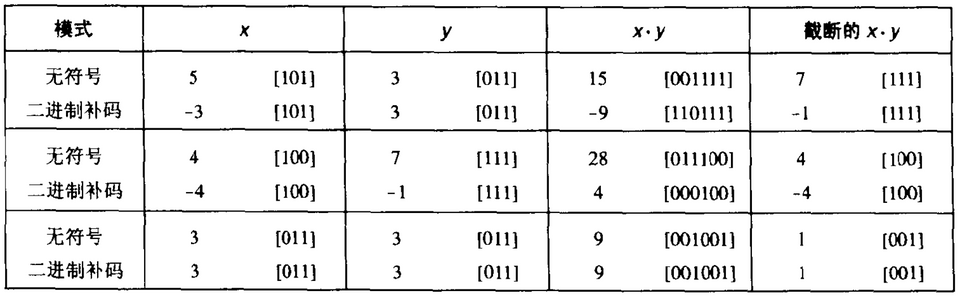
乘以二的幂
一般操作可能溢出,位移不会,x << k == x *
除以二的幂
负的不正确,-5 / 2 = 1011 >> 1 = 1101 = -3,所以 (x < 0 ? (x + (1 << k) - 1) : x) >> k,-5 / 2 = (-5 + (1 << 1) - 1) >> 1 = 1100 >> 1 = 1110 = -2
浮点
二进制小数
限制:只能表示 ,其他的需要无限循环;范围限制
IEEE 浮点表示
32 位 float:s 占 1 位,exp 占 k=8 位,frac 占 23 位
对应 double: exp 占 k=11 位,frac 占 52 位
Bias = (32 位是 127,64 位是 1023)
规格化值:exp 不全为 0 或 1 时,
非规格化值:exp 全为 0 或 1 时,(提供非规格化值平滑转换为规格化值)
特殊数值:当 exp 全为 1 时,frac 全为 0 表示无穷,frac 非零表示 NaN
以下 8 位 k=4,Bias=7
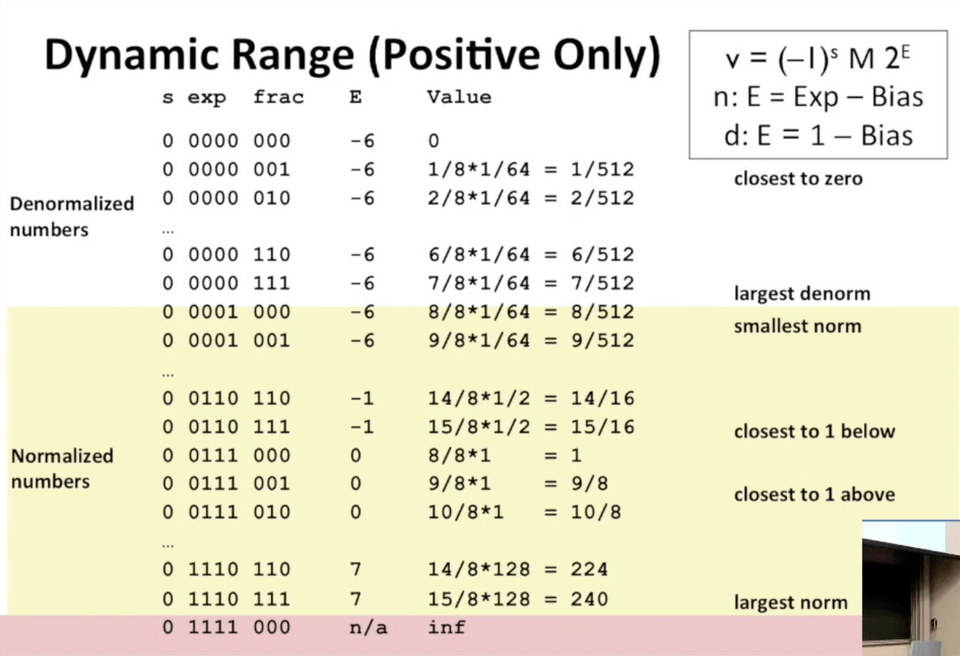
舍入
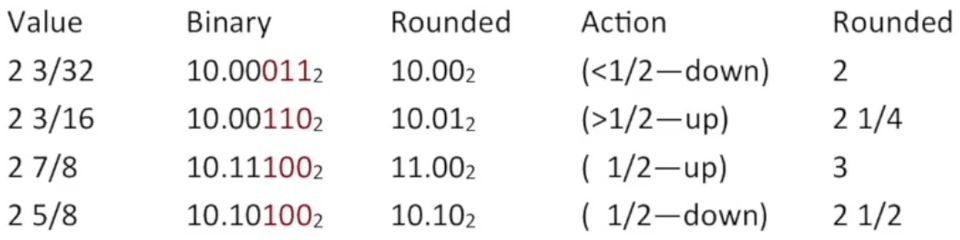
data lab
// TODO: data lab