构造数据抽象

复合数据、抽象屏障、模糊“过程”和“数据”的划分、符号表达式（扩大语言的表述能力）、通用型操作

数据抽象导引

抽象屏障

1(define (make-vector x y) (cons x y)) ; (define make-vector cons)
2(define (getx x) (car x)) ; (define getx car)
3(define (gety x) (cdr x)) ; (define gety cdr)

1(define make-line cons)
2
3(define start car)
4(define (startx line)
5  (getx (start line)))
6(define (starty line)
7  (gety (start line)))
8
9(define end cdr)
10(define (endx line)
11  (getx (end line)))
12(define (endy line)
13  (gety (end line)))
14
15(define (length line)
16  (sqrt (add (sub endx startx) (sub endy starty))))

1-----( 图形程序 )-----
2图形、对图形的操作
3-----( 线 )------
4make-line end start endx startx...
5-----( 向量 )------
6make-vector getx gety...
7-----( 有序对 )-----
8cons car cdr...

数据意味着什么

有序对的创建：

1(define (cons x y)
2  (lambda (pick)
3    (cond ((= pick 0) x)
4          ((= pick 1) y)
5          (else (error "Argument not 0 or 1 -- cons" pick)))))
6
7(define (car pair) (pair 0))
8(define (cdr pair) (pair 1))

cons 返回一个过程，car cdr 对过程进行了操作，有序对的数据结构其实是一种过程，模糊“过程”和“数据”的划分

1(define (cons x y)
2  (lambda (m) (m x y)))
3
4(define (car z)
5  (z (lambda (x y) x)))
6
7(define (car z)
8  (z (lambda (x y) y)))

丘奇计数

层次性数据和闭包性质

闭包：通过某种数据对象的操作，组合起来得到的数据对象还可以通过同样的操作进行组合

闭包另一种含义：一种为表示带有自由变量的过程而用的实现技术

序列的表示

1(list 1 2 3 4)
2
3; 语法糖
4; (cons 1
5;   (cons 2
6;     (cons 3
7;       (cons 4 nil))))

nil 空表，是拉丁文“nihil”的缩写，表示“什么也没有”

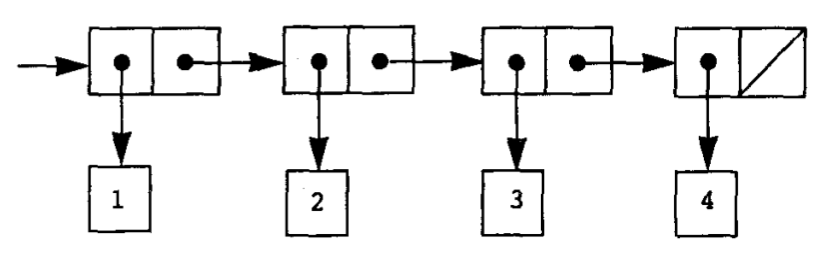
list 是一个过程，返回 (1 2 3 4) 表

1(define ls (list 1 2 3 4))
2(car ls) ; 1
3(cdr ls) ; (2 3 4)

对表的操作：

1; 根据下标返回元素
2(define (list-ref ls n)
3  (if (= n 0)
4    (car ls)
5    (list-ref (cdr ls) (- n 1))))
6
7; 返回表的长度
8(define (length ls)
9  (if (null? ls)
10    0
11    (+ 1 (length (cdr ls)))))
12
13(define (length ls)
14  (define (iter ls count)
15    (if (null? ls)
16      count
17      (iter (cdr ls) (+ count 1))))
18  (iter ls 0))
19
20; 添加
21(define (append list1 list2)
22  (if (null? list1)
23    list2
24    (cons (car list1) (append (cdr list1) list2))))
25
26; 反转
27(define (reverse lst)
28  (define (iter remained-items result)
29    (if (null? remained-items)
30      result
31      (iter (cdr remained-items)
32        (cons (car remained-items) result))))
33  (iter lst '()))

对表的映射：

1(define (map proc ls)
2  (if (null? ls)
3    (list) ; nil
4    (cons (proc (car ls))
5          (map proc (cdr ls)))))

Scheme 标准提供了一个 map，更具有一般性，以一个取 n 个参数的过程和 n 个表为参数，将过程应用于所有表的第一个元素，之后应用于所有表的第二个参数…… 最后返回所有结果的表
1(map + (list 1 2 3) (list 40 50 60) (list 700 800 900)) ; (741 852 963)

剩余参数：

1(define (f x y . z) (display z))
2(f 1 2 3 4 5) ; (3 4 5)

层次性结构

1(cons (list 1 2) (list 3 4))

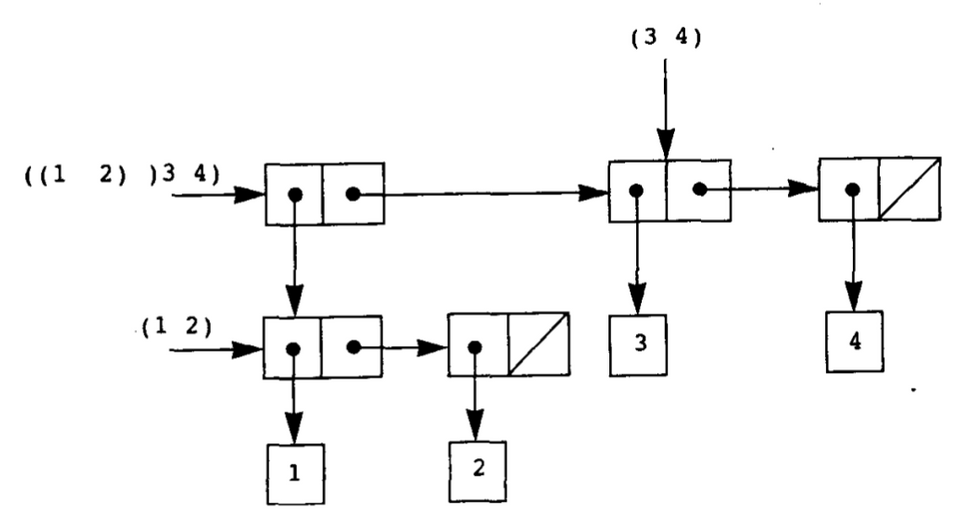
1(define (count-leaves x)
2  (cond ((null? x) 0)
3        ((not (pair? x)) 1)
4        (else (+ (count-leaves (car x))
5                 (count-leaves (cdr x))))))
6
7(define (scale-tree tree factor)
8  (map (lambda (tree)
9         (if (pair? tree)
10             (scale-tree tree factor)
11             (* tree factor)))
12       tree))

序列作为一种约定的界面

1(define (sum-odd-squares tree)
2  (cond ((null? tree) 0)
3        ((not (pair? tree))
4          (if (odd? tree) (square tree) 0))
5        (else (+ (sum-odd-squares (car tree))
6                 (sum-odd-squares (cdr tree))))))
7
8(define (evens-fibs n)
9  (define (next k)
10    (if (> k n)
11        (list)
12        (let ((f (fib k)))
13          (if (even? f)
14              (cons f (next + k 1))
15              (next (+ k 1))))))
16  (next 0))

第一个过程：

枚举一棵树的树叶
过滤选出奇数
求平方
累加

第二个过程：

枚举 0-n 的整数
对每个整数计算 fib 数列
过滤选出偶数
用 cons 累积结果

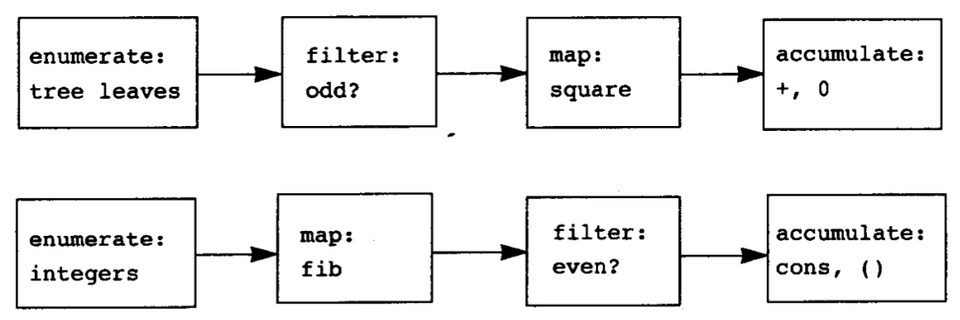
只写出第一个过程的操作：

1(define (enum-tree tree)
2  (cond ((null? tree) (list))
3        ((not (pair? tree)) (list tree))
4        (else (append (enum-tree (car tree))
5                      (enum-tree (cdr tree))))))
6
7(define (sum-odd-tree tree)
8  (accumulate +
9              0
10              (map square
11                   (filter odd?
12                           (enum-tree tree)))))

符号数据

引号

引用

1(define a 1)
2(define b 2)
3
4(list a b) ; (1 2)
5(list 'a 'b) ; (a b)
6(car '(a b c)) ; a
7'() ; nil 空表

1; eq? 是判断两个参数是否指向同一个对象，如果是才返回#t
2; equal? 是判断两个对象是否具有相同的结构并且结构中的内容是否相同
3(eq? 'this 'this) ; #t
4(eq? '(this is a list) '(this is a list)) ; #t
5(equal? '(this is a list) '(this is a list)) ; #t

符号求导

1(define (deriv exp var)
2  (cond ((number? exp) 0) ; 是否常数
3        ((variable? exp) ; 是否变量
4          (if (same-variable? exp var) 1 0)) ; 是否是同一个变量
5        ((sum? exp) ; 是否是和式
6          (make-sum (deriv (addend exp) var) ; addend 求 exp 的被加数
7                    (deriv (augend exp) var))) ; augend 求 exp 的加数
8        ((product? exp) ; 是否是乘式
9          (make-sum
10            (make-product (multiplier exp) ; multiplier 求 exp 的被乘数
11                          (deriv (multiplcand exp) var)) ; multiplcand 求 exp 的乘数
12            (make-product (deriv (multiplier exp) var)
13                          (multiplcand exp))))
14        (else (error "unknown expression type -- DERIV" exp))))

1(define (variable? x) (symbol? x))
2
3(define (same-variable? v1 v2)
4  (and (variable? v1) (variable? v2) (eq? v1 v2)))
5
6(define (sum? exp)
7  (and (pair? exp) (eq? (car exp) '+)))
8
9(define (make-sum e1 e2) (list '+ e1 e2))
10
11(define (addend exp) (cadr exp))
12
13(define (augend exp) (caddr exp))
14
15(define (product? exp)
16  (and (pair? exp) (eq? (car exp) '*)))
17
18(define (multiplier exp) (cadr exp))
19
20(define (multiplcand exp) (caddr exp))
21
22(define (make-product e1 e2) (list '* e1 e2))

1(deriv '(+ x 3) 'x) ; (+ 1 0)
2(deriv '(* (* x y) (+ x 3)) 'x) ; (+ (* (* x y) (+ 1 0)) (* (+ (* x 0) (* 1 y)) (+ x 3)))

仍然可以简化，修改 make-sum 和 make-product 判断 e1 e2 是否为数字，是则化简

AHABHGK