构造计算过程抽象

计算过程的 Lisp 描述（称为过程）本身又可以作为 Lisp 的数据来表示和操作

程序设计的基本元素

将简单的认识组合成更复杂认识的方法方面，每一种强有力的语言都提供三种机制：

基本表达形式：用于表达语言所关心的最简单的个体
组合的方法：从简单的元素构造出复杂的元素
抽象的方法：为复杂的元素命名，并将它们当作单元去操作

表达式

前缀表达式：

1(+ (* 3
2      (+ (* 2 4)
3        (+ 3 5)))
4  (+ (- 10 7)
5    6))

完全适用于可能带有任意个实参的过程

命名和环境

1(define pi 3.1415926)

一个 Lisp 程序通常总是由一大批相对简单的过程组成

可以将值与符号关联，而后又提取出这些值，这意味着解释器必须维护某种存储能力，以便保持名字 - 值的对应关系，这种储存被称为环境

组合式的求值

求值该组合式的各个子表达式
将作为最左子表达式（运算符）的值的那个过程应用与实际参数（其它子表达式的值）

1(* (+ 2 (* 4 6))
2  (+ 3 5 7))

数的值就是它们表示的数值
内部运算符的值就是能完成相应操作的机器指令序列
其他名字的值就是在环境中关联这一值的那个对象

1(define x 3) ; 表示符号 x 关联另一个值 3
2
3(define (x) 3) ; 表示过程 x

复合过程

定义过程

1(define (<name> <formal parameters>) <body>)

过程应用的代换模型

正则序求值：

完全展开而后归约

1(define (square x) (* x x))
2
3(+ (square 3) (square 2))
4; => (+ (* 3 3) (* 2 2)) 完全展开
5; => (+ 9 4) => 11 归约（reduce）求值

应用序求值：

先求值参数而后应用

1(define (square x) (* x x))
2
3(+ (square 3) (square 2))
4; => (+ (square 3) (* 2 2))
5; => (+ (square 3) 4)
6; => (+ (* 3 3) 4)
7; => (+ 9 4) => 11

Lisp 采用应用序求值，避免一些重复求值，提高效率

thunk、求值策略（传值调用 call by value、传名调用 call by name）

条件表达式和谓词

1; (cond (<p1> <e1>)
2;   (<p2> <e2>)
3;   (<p3> <e3>))
4
5(define (abs x)
6  (cond ((> x 0) x)
7    ((= x 0) 0)
8    ((< x 0) (- x))))

\<p>：谓词，返回 #t 或 #f，风格上一般在谓词后面加 ? 表示

当解释器检查谓词的值时，#f 解释为假，其余的都解释为真，在逻辑上 #t 是不需要的，只是为了方便

1(define (abs x)
2  (cond ((< x 0) (- x))
3    (else x)))
4
5; (if <predicate> <consequent> <alternative>)
6(define (abs x)
7  (if (< x 0)
8    (- x)
9    x))

逻辑运算符：

1(and <e1> <e2>)
2(or <e1> <e2>)
3(not <e>)

过程作为黑箱抽象

牛顿法求平方根

1(define (sqrt x)
2  (define (average a b)
3    (/ (+ a b)
4      2))
5  (define (square x)
6    (* x x))
7  (define (improve guess)
8    (average guess (/ x guess)))
9  (define (good-enough? guess)
10    (< (abs (- (square guess) x))
11      .001))
12  (define (try guess)
13    (if (good-enough? guess)
14      guess
15      (try (improve guess))))
16  (try 1))
17
18; sqrt
19; └── try
20;     ├── good-enough?
21;     │   ├── square
22;     │   └── abs
23;     └── improve
24;         └── average
25
26(display (sqrt 5))

过程与它们所产生的计算

线性的递归和迭代

递归计算过程：由一个推迟执行的运算链条所刻画，链条用于保存需要的信息量，这个链条越长，其中“隐含”保存的信息就越多

由于这个链条长度随 n 值线性增长（正比与 n）所以也叫线性递归

1(define (factorial n)
2  (if (= n 1)
3    1
4    (* n (factorial (- n 1)))))
5
6; (factorial 5)                          /|\ time: O(n)
7; (* 5 (factorial 4))                     |
8; (* 5 (* 4 (factorial 3)))               |
9; (* 5 (* 4 (* 3 (factorial 2))))         |
10; (* 5 (* 4 (* 3 (* 2 (factorial 1)))))   |
11; (* 5 (* 4 (* 3 (* 2 1))))               |
12; (* 5 (* 4 (* 3 2)))                     |
13; (* 5 (* 4 6))                           |
14; (* 5 24)                                |
15; 120
16; -------------------------------------> space: O(n)

迭代计算过程：其状态可以用固定数目的状态变量描述的计算过程

由于计算步骤随 n 线性增长（正比于 n）所以也称线性迭代

1(define (factorial n)
2  (define (fact-iter product counter)
3    (if (> counter n)
4      product
5      (fact-iter
6        (* product counter)
7        (+ counter 1))))
8  (fact-iter 1 1))
9
10; (factorial 5)     /|\ time: O(n)
11; (fact-iter 1 1)    |
12; (fact-iter 1 2)    |
13; (fact-iter 2 3)    |
14; (fact-iter 6 4)    |
15; (fact-iter 24 5)   |
16; (fact-iter 120 6)  |
17; 120
18; -------------------> space: O(1)

尾递归：用递归过程描述的在常量空间中执行的迭代计算过程

树形递归

斐波那契数列

1(define (fib n)
2  (cond ((= n 0) 0)
3    ((= n 1) 1)
4    (else (+ (fib (- n 1)) (fib (- n 2))))))

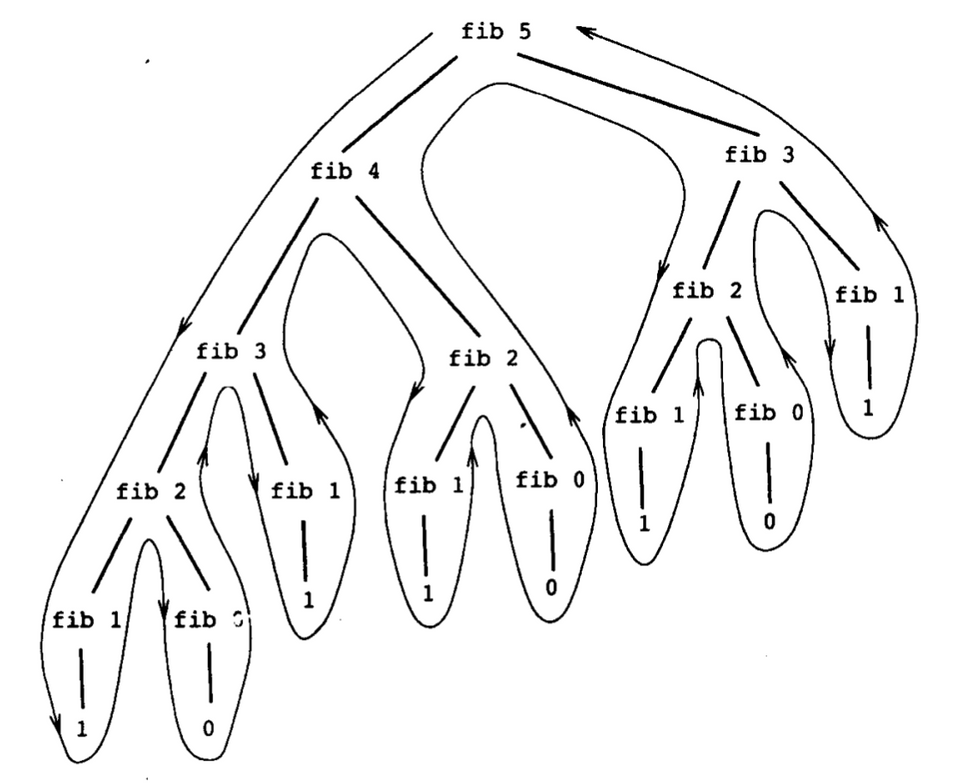
space: O(n) time: O(fib(n))

1; a => a + b
2; b => a
3
4(define (fib n)
5  (define (fib-iter a b count)
6    (if (= count 0)
7      b
8      (fib-iter (+ a b) a (- count 1))))
9  (fib-iter 1 0 n))
10
11; (fib 5)
12; (fib-iter 1 0 5)
13; (fib-iter 1 1 4)
14; (fib-iter 2 1 3)
15; (fib-iter 3 2 2)
16; (fib-iter 5 3 1)
17; (fib-iter 8 5 0)
18; 5

增长的阶

O(n) O(n ^ 2) O(log2 n)

其中的 n、n^2、log2 n 就是阶

用高阶过程做抽象

过程作为参数

$\sum-{n=a}^bf(n)=f(a)+...+f(b)$

1(define (sum-int a b)
2  (if (> a b)
3    0
4    (+ a (sum-int (+ 1 a) b))))
5
6(define (sum-cubes a b)
7  (if (> a b)
8    0
9    (+ (cube a) (sum-cubes (+ 1 a) b))))
10
11(define (pi-sum a b)
12  (if (> a b)
13    0
14    (+ (/ 1.0 (* a (+ a 2))) (pi-sum (+ a 4) b))))

抽象过程，并使用 lambda：(lambda (<formal-parameters>) <body>)

1(define (sum term a next b)
2  (if (> a b)
3    0
4    (+ (term a) (sum term (next a) next b))))
5
6(define (sum-int a b)
7  (define (identity x) x)
8  (define (inc x) (+ 1 x))
9  (sum identity a inc b))
10
11(define (sum-cubes a b)
12  (sum (lambda (x) (* x x x)) a (lambda (x) (+ 1 x)) b))
13
14(define (pi-sum a b)
15  (sum (lambda (x) (/ 1.0 (* x (+ 2 x))))
16    a
17    (lambda (x) (+ 4 x))
18    b))

(define (inc x) (+ 1 x)) == (define inc (lambda (x) (+ 1 x)))

局部变量

$f(x,y)=x(1+xy)^2+y(1-y)+(1+xy)(1-y)$

$a=(1+xy)$

$b=(1-y)$

$f(x,y)=a^2x+by+ab$

1(define (f x y)
2  (define (f-helper a b)
3    (+ (* x (* a a))
4       (* b y)
5       (* a b)))
6  (f-helper (+ 1 (* x y))
7            (- 1 y)))

1(define (f x y)
2  ((lambda (a b)
3    (+ (* x (* a a))
4       (* b y)
5       (* a b)))
6    (+ 1 (* x y))
7    (- 1 y)))

let:

1; (let ((<var1> <exp1>)
2;       (<var2> <exp2>)
3;       ...
4;       (<varn> <expn>))
5;   <body>)
6; ==
7; ((lambda (<var1> <var2> ... <varn>)
8;   <body>)
9;   <exp1>
10;   <exp2>
11;   ...
12;   <expn>)
13
14(define (f x y)
15  (let ((a (+ 1 (* x y)))
16        (b (- 1 y)))
17    (+ (* x (* a a))
18       (* y b)
19       (* a b))))

1(define (f x y)
2  (define a (+ 1 (* x y)))
3  (define b (- 1 y))
4  (+ (* x (* a a))
5       (* y b)
6       (* a b)))

一般 let 用于定义值，define 用于定义过程

过程作为一般性方法

不动点： $f(x) = x$

通过某个初始值猜测，之后反复应用 $f(x)、f(f(x))、f(f(f(x)))$

1(define (fixed-point f first-guess)
2  (define (close-enough? v1 v2)
3    (< (abs (- v1 v2)) 0.00001))
4  (define (try guess)
5    (let (next (f guess))
6      (if (close-enough? guess next)
7        next
8        (try next))))
9  (try first-guess))

过程作为返回值

求导： $df(x)=\frac{f(x+dx)-f(x)}{dx}$

1(define (deriv f)
2  (let ((dx 0.00001))
3    (lambda (x)
4      (/ (- (f (+ x dx)) (f x)) dx))))
5
6(define (cube x) (* x x x))
7
8((deriv cube) 5)